댓글 쓰기 권한이 없습니다. 로그인 하시겠습니까?
|
Pi
2016.12.05 16:21
키르히호프의 법칙
조회 수 27238 댓글 0
구스타프 키르히호프(Gustav Kirchhoff)가 구한 전기 회로에 대한 법칙이다. 1845년 구스타프 키르히호프가 처음으로 기술한 전기회로에서의 전하량과 에너지 보존을 다루는 2개의 이론식이다. 이 이론식은 전기공학분야에서 폭넓게 사용되고 또한 줄여서 키르히호프의 규칙(Kirchhoff's rules)또는 키르히호프의 법칙이라 불린다(키르히호프 법칙 용어 참조). 두 개의 회로 이론들은 맥스웰 방정식(Maxwell's equations)으로부터 직접적으로 유도될 수도 있다. 명실공히 전기회로계의 뉴턴 법칙 키르히호프의 전기회로 법칙은 전기회로에 있어서 전압이나 전류를 구하기 위한 법칙이다. 구스타프 키르히호프가 19세기에 정립하였으며, 이는 전하량 보존과 에너지 보존과 관계가 있다. 경우에 따라서는 전기회로의 방정식을 세우는 데 필수적인 도구라 하여 '키르히호프의 규칙'이라고도 한다. 그러한 이유로 전기, 전자쪽을 전공하는 학생들은 필수적으로 알아야하는 공식이다. 이 공식을 이용하면 많은 식을 유도할 수 있어 이후 배울 전기, 전자 이론에서 외워야할 식의 수를 줄여준다. 1. 키르히호프 제 1법칙(Kirchhoff's Current Law, KCL) 전하량 보존 법칙. 전류 규칙 혹은 분기점 법칙.
위 식에서 Ik 항은 들어오는 전류이면 (+), 나가는 전류이면 (-) 부호로 정해진다. 물론 그 반대로 정해도 상관 없다. 여기서 '한 지점'이란 꼭 분기점일 필요는 없다. 단순히 '선로 상의 한 지점'에서도 들어오는 전류와 나가는 전류의 크기는 동일하며, 해당 지점에서는 전하가 쌓이지 않는다. 흔히들 하는 오해가 이름 때문인지 전류가 나뉘는 분기점에서만 성립한다고 생각하는데, 전하량 보존 법칙을 생각해보면 그냥 단일 도선의 어떤 지점에서든지 들어온 전류가 나가는 전류와 같다는 것을 알수 있다. 사용되는 곳: 키르히호프의 매트릭스 버전이 SPICE와 같은 모든 반도체 디자인 회로 시뮬레이션 소프트웨어의 기본 법칙으로 적용된다. (지금 보이는 이 간단한 식이 이후에 모든 선형회로의 강력한 기초 법칙으로 모든 회로를 해석하고 반도체를 디자인하는 기본 법칙으로도 적용된다.) 2. 키르히호프 제 2법칙(Kirchhoff's Voltage Law, KVL) 에너지 보존 법칙. 고리 규칙, 루프의 법칙.
전기회로 내의 모든 지점은 전기 퍼텐셜을 지정할 수 있다. 한편 어떤 '닫힌 경로'를 따라 이동할 때 전기 퍼텐셜의 변화는 제자리로 돌아오고, 이것이 위 수식에 써진 바와 같다. 이것이 키르히호프의 전압 법칙이다.
이 법칙은 에너지의 인가와 출력, 공급과 소비의 포텐셜장(에너지보유장) 기초 원칙이 된다.(루프안에서의 에너지는 소멸되지 않는 다는 가정 하에서이다.) 인가된 전압 포텐셜, 완전히 폐쇄된 루프의 전하량 증가하거나 감소하지 않으며, 처음 인가된 전하량을 유지한다. 한계점 패러데이의 전자기 유도 법칙은 자기장이 변하는 곳에 있는 도체에 전위차(전압)가 발생한다고 하였다. 실제적으로 전자기장에서는 전하량 보존의 법칙이 성립되지 않는다. 실질적인 회로의 상태에서는 완전하고 완벽한 폐쇄 회로를 만들수 없으면, KVL에 존재하는 회로는 존재하지 않는다. 참고로 통상 '고도'를 정할 때 특정한 지점의 고도를 기준으로 삼고 다른 지점의 고도를 측정한다. 전기회로도 마찬가지다. 전기 회로 내의 특정 지점의 전기 퍼텐셜을 지정하면, 다른 지점의 전기 퍼텐셜을 구할 수 있다. 한 전자(전하운반자)의 입장에서 볼 때, 전자는 전원을 거치면서 에너지를 받고, 회로 소자를 지나면서 일을 한다. 이 때 에너지의 출입은 전자의 전하량과 전기 퍼텐셜의 변화의 곱으로 나타난다. 전자가 제자리로 돌아올 때 같은 퍼텐셜 준위로 돌아오므로, 들어온 에너지와 나간 에너지는 동일해야 한다. 이는 전원이 일한 만큼 에너지가 회로 소자로 전달된다는 뜻이 된다. 그러니까,
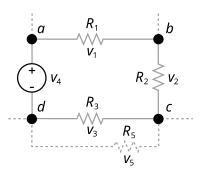
이때의 R1을 구한다면, - 옴의 법칙 : V = IR + 1Ω의 정의 : 1V가 1A로 흐르는 회로의 저항 + V 볼트 : 볼타르 전지를 사용했기 때문에 볼트가 됨 + A 암페어 : 암페르가 전선에 흐르는 자기장의 세기를 통해 간접적으로 정의함. - KCL에 의해서 R1에 걸리는 전류는 20mA가 되고, KVL에 의해 R1에 걸리는 전압은 5V-2V=3V 가됨. 옴의 법칙에 의해 R1 = V/I = 3V/0.02A = 150Ω 이 됨 Dreamy의 코드 스크랩내가 모으고 내가 보는
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


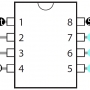 ATTINY85 PIN정보, Data sheet
ATTINY85 PIN정보, Data sheet